FBAR Cards Insight

December 6, 2023

Fbar Cards is a card game designed to help researchers gain initial insights on informative hypothesis testing for ANOVA models as implemented in the 'restriktor' R package. The game goes like this:

  • Set the "difficulty level" n
  • Click Start/Restart Game to deal an n x n grid of cards from a standard 52 card deck
  • For each row you can either:
  • Leave the cards as is
  • Swap two cards within the row
  • ONLY 1 swap is allowed per row
  • Click Score Game


In this game, the columns represent groups for an ANOVA analysis using an informative hypothesis testing framework where:


'col1 < col2 < col3'


is the constraint. As such, the user is expected to use their moves in each row to try to order the cards in increasing order.


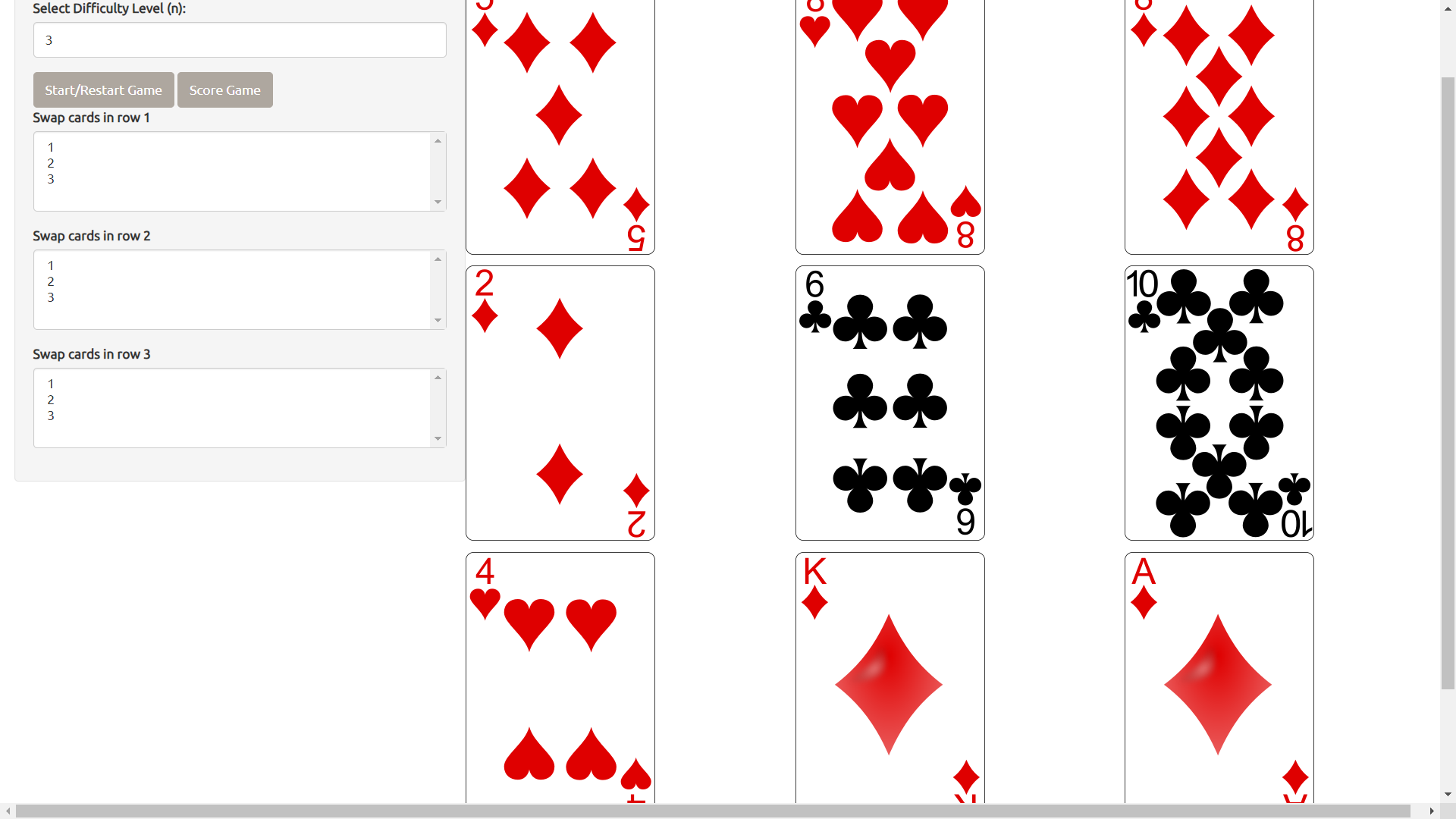
Here is a sample hand of the game on level n = 3. After I click Start/Restart Game, I have the following grid:


With this hand I made the following moves:



  • Row 1: I did nothing in row 1. This was a mistake on my part; I forgot that hearts is defined as a higher value than diamonds. See the standard_deck function of 'mmcards' to see how the deck was defined (clubs < diamonds < hearts < spades).
  • Row 2: Swapped 10 and 2
  • Row 3: Swapped Ace and 4


This was the final hand:

With this hand, I then clicked Score Game and obtained:

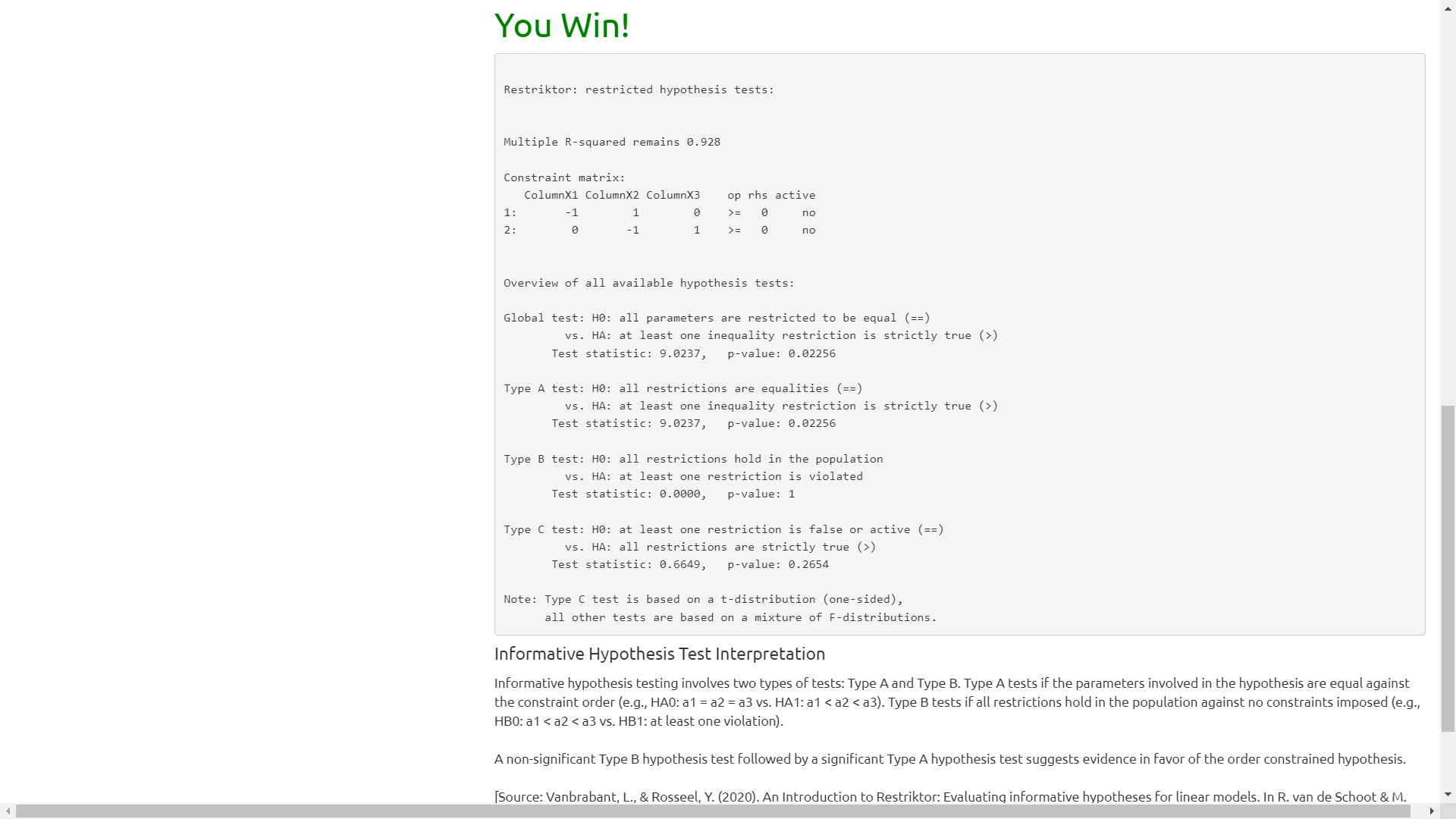
At this point, we can get into the insight.

Insight: Focus on the Edges

Since I'm only allowed one swap per row, when I play at higher difficulty levels, my main (and often only) focus is on making sure the card in column n has the largest value in the row. I've found that this strategy is surprisingly efficient.


In the paper Constrained statistical inference: sample-size tables for ANOVA and regression I came across a small passage which helps me understand what is going on here:


"In particular we would like to know about the power when the means are not perfectly in line with the ordered hypothesis

...

the power for Hypothesis test Type A (HA0 vs. HA1) is largely dominated by the extremes (here the first and last mean). This means that, irrespective of the deviations of the two middle means, the power is almost not affected."


Keep in mind that to "Win" we need to fail to reject the null hypothesis on the Type B test and reject the null hypothesis on the Type A test.

Who Said It Best Episode 1: Daniel McNeish

August 19, 2024
Mighty Metrika focuses on statistical methods and mathematics for the analysis of small sample size data. As such, the project runs the risk of people with small sample sizes using tools and methods from mightymetrika.com and becoming over confident in their results because they used "small sample size methods." The long term rigorous goal to combat this disservice is to host citizen science projects, include simulation function in R packages, and share simulation results from the literature and from mightymetrika.com tools through blogs. A short and quick way to combat misuse is through the Who Said It Best series. The series will share some of the best warnings from the small sample size statistical literature. In the Conclusion section of Daniel McNeish's paper Challenging Conventional Wisdom for Multivariate Statistical Models With Small Samples he shares a clear and wonderfully worded warning:

Resources for Building R Shiny x PostgreSQL x AWS EC2 Apps

June 25, 2024
This is a quick blog post to list some of the essential resources that I needed to get a citizen science app up and running. The app uses: R Shiny PostgreSQL Pool AWS EC2 The post is basically a way for me to bookmark resources that I found useful and also as a way to say thank you to the folks that put these resources up online.

BFfe: Test Update

June 10, 2024
In 'mmibain' v0.2.0, the unit tests are passing at the moment, but on r-devel-linux-x86_64-debian-clang it really seems to be hit or miss. I believe that when the test fails it is do to the new BFfe function which is a case-by-case type implementation of ' bain ' for linear models; however, I used a unit test which relies on a synthetic data set where I generated random numbers and then just used the rep() function to group observations by participants. As such, the data generating process does fit the statistical model and sometimes the random data set that is generated does not make it through bain::bain() without error. I have already changed the unit test and corresponding Roxygen2 documentation example on the Mighty Metrika GitHub and this blog post will walk through the new data and model. But just for further context, here is the original code that sometimes runs through and sometimes throws and error.
More Posts